
Como parte del proceso de titulación de la carrera de Educación Diferencial de la Universidad Alberto Hurtado, Soledad Acuña Perales desarrolló la Investigación Acción “Diseño, implementación y evaluación de una estrategia basada en la resolución de problemas para el aprendizaje matemático” que consta de una secuencia didáctica realizada durante 2018 en un colegio municipal de la comuna de la Florida con un grupo de estudiantes de 2° año básico que requería apoyos adicionales en esta área. A través de la teoría de situaciones didácticas (Brousseau) y un enfoque inclusivo, su trabajo buscó contribuir al aprendizaje con una propuesta alternativa de enseñanza de la matemática.
A partir de una observación y diagnóstico inicial, se pudo apreciar que en clases de matemática, predominaban prácticas de enseñanzas tradicionales. Los contenidos eran transmitidos por el docente a través de procedimientos únicos de resolución, para que luego los estudiantes replicaran lo aprendido con foco en la ejercitación de cálculos rutinarios y descontextualizados, poco significativos y con nulo espacio para que pudieran compartir sus experiencias, inquietudes, dificultades y estrategias de resolución. Con esta forma de enseñanza, se observó a un grupo de 8 estudiantes que manifestaban dificultades para resolver problemas de tipo aditivo, es decir, adiciones y sustracciones utilizando el algoritmo tradicional o mediante estrategias no convencionales.
La primera etapa de esta investigación-acción consistió en una evaluación diagnóstica, a través de preguntas abiertas de resolución para determinar la comprensión y las principales estrategias utilizadas por los estudiantes en problemas aditivos directos, inversos y de comparación. Se apreció que los estudiantes lograban comprender y resolver adiciones principalmente a través de representaciones pictóricas y apoyo digital y había menor uso de representaciones simbólicas (algoritmo). También se observó más dificultad para comprender y resolver problemas directos e inversos de sustracción. A partir de este diagnóstico, se pudo concluir que a pesar de utilizar variadas estrategias para resolver diferentes problemas, permanecían dificultades para comprender los enunciados y utilizar estrategias apropiadas acordes a cada situación planteada, por lo que el aprendizaje matemático en el campo aditivo aún no se encontraba consolidado.
A partir de las evidencias obtenidas en la primera etapa, se desarrolló una experiencia de aprendizaje basado en la resolución de problemas aditivos de tipo directo e inverso (de cambio y composición) y de comparación. Se trabajó a partir del contexto “La feria de diversiones” donde los problemas a resolver estaban orientados a variados juegos típicos. La secuencia didáctica, se implementó en 7 sesiones de clases. Se estructuró en base a situaciones de acción, formulación y validación de las estrategias y conocimientos de los estudiantes, Se pensó en instancias de resolución individual a partir de estrategias propias, para luego compartirlas y discutir sobre ellas, validando o reformulando sus conocimientos y estrategias utilizadas (Brousseau 1982, Charnay 1994, Chamorro 2005). Además, se propiciaron instancias de aprendizaje a partir de la valoración del error, preguntas de tipo abiertas y momentos de trabajo colectivo que favoreció la participación y colaboración de los estudiantes para el aprendizaje entre pares. Finalmente, se aplicó una evaluación final para contrastar los aprendizajes de los estudiantes antes y después de la aplicación de la secuencia didáctica.
A partir de la experiencia implementada se pudo concluir que los estudiantes continuaron utilizando diversas estrategias de resolución principalmente de tipo pictóricas. Sin embargo, a través de las diferentes sesiones comenzaron a utilizar más estrategias de tipo simbólico (algoritmo) y digital, pues, al compartirlas constantemente en clases, los alumnos aprendían nuevas formas de resolver problemas que más adelante las utilizaban como recursos propios. Por otra parte, se observaron avances en torno a la comprensión de los problemas trabajados, ya que a través de las sesiones, los alumnos lograban reconocer y relacionar la operación que implicaba cada una de la situaciones planteadas independientemente de la forma o estrategias de resolución empleada por cada estudiante, logrando establecer relaciones entre la respuesta dada y la pregunta central de cada problema.
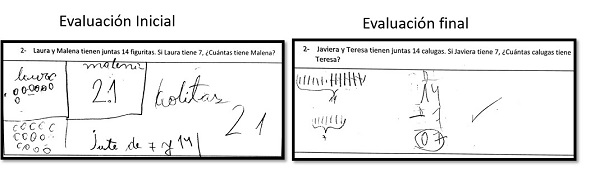

La investigación-acción contempló una tercera etapa, donde se contrastan los resultados de la evaluación diagnóstica. Los avances fueron evidentes. Se observó que gran parte de los niños incorporó mayor variedad de estrategias y representaciones para resolver. Asimismo, se pudo concluir que algunos conocimientos necesitaban consolidarse en secuencias que se extiendan más en el tiempo.
En conclusión, enseñar matemáticas desde un enfoque de resolución de problemas beneficia el aprendizaje de estudiantes diversos, pues implica que no todos los alumnos aprendan lo mismo en un determinado tiempo, sino más bien, que cada estudiante construya su aprendizaje a partir de lo que ya sabe (conocimientos previos) y avance acorde a su ritmo de aprendizaje. Por otra parte, la resolución de problemas implica aprender matemáticas a partir de la interacción con otros, principalmente con sus pares, donde cada estudiante mantiene un rol activo, generando y compartiendo diversas estrategias, comparando y validando sus propios conocimientos, para luego reformular sus aprendizajes a partir de la discusión /conversación con sus pares, y mediado por el docente. Es importante valorar desde este enfoque, las diferentes estrategias utilizadas por los estudiantes, el error como una instancia de aprendizaje y los momentos de interacción entre pares, dando espacio para que discutan, compartan y fundamenten cada una de sus estrategias y conocimientos, generando un rol y participación activa de los alumnos.
Desde la perspectiva de la educación diferencial, los resultados de esta investigación acción señalan que es posible generar cambios en la enseñanza y aprendizaje de los estudiantes, principalmente de aquellos que presentan mayores dificultades y que en muchas ocasiones suele ser una problemática propia de los alumnos (dificultades centrada en el estudiante) y que no se sabe cómo abordar por parte de los docentes. Sin embargo, este trabajo muestra que generar aprendizajes en los estudiantes depende considerablemente de las prácticas de enseñanza que promueva cada docente en las aulas, las interacciones y el grado de participación e involucramiento que se les otorgue a los estudiantes en cada una de las actividades planteadas. Las clases de matemáticas basadas en la resolución de problemas son una buena práctica para implementar a diario en las aulas, pues promueven la participación y aprendizaje de todos los estudiantes, sin dejar de lado a aquellos que presentan mayores dificultades en esta asignatura.
Para ver su trabajo completo, descarga aquí

